Entity Resolution
machine-learning tutorial project Introduction
The serverless components of the Entity Resolution Application are described in another post. For more detail the subject of Entity Resolution, I wrote this primer for my NYU class. For the specific implementation, the methodology is described below.
Methodology I
The model is based on Norvig's spelling corrector. The general equation, using Bayes Theorem to disambiguate sub-problems: $$\{c|P(c|\epsilon)>\theta\}\longrightarrow \{c|P(\epsilon|c)P(c)>\theta\}$$
There are four parts:
- Selection Model: $>\theta$. This is the threshold by which two entities are considered a match. This should be based on some training examples of labeled data.
- Candidate Model: $\{c\}$. Set of candidates. Picking an appropriate set of candidates is the crux of the entity resolution methodology. Too few candidates will result in low recall. Too many will lead to $n^2$ computations making it infeasible. In my current approach, I am only considering two candidates that are inputted by the users.
- Error Model: $P(\epsilon|c)$. There are numerous methods to model this. For example, a machine learning model. In this case, the model is number of correct divided by length of bigger word. An imperfect measure to say the least.
- Entity Model: $P(c)$. Assumed to be 1 for now. When properly implemented, will correct for common/rare instances.
The algorithm does basic treatment to the two input words (lower case, removing punctuation and words like inc, corp, etc. Then the model described above is applied to calculate the probabilty of the match. Entity Resolution is a complex, deep topic. This application barely scratches the surface.
Methodology II
This model uses lookups rather than direct matching, which allows for the circumstance that a company name may have different letters or words, but still refer to the same entity, like Meta Platforms and Facebook.
General Framework
A lookup table is constructed of keys that map to a specific company, where the company name is predefined. There is a probability of association between the key and the company, as defined in the next section. When a user inputs two entities, they are (probabilistically) associated with a key and in turn a company name. Thus, there are two major parts of the framework. First, building the look-up table. Second, utilizing the look-up table to identify matches and non-matches.
Building the Look-Up Table
In this model, a company is represented by a document or a set of documents. To start, I use its Wikipedia page. Alternatively, annual reports, SEC filings, or an aggregation of all of them can be used. Then a key-value store is constructed by:
- It starts with a set of company names to iterate over. I use the SP500 list, which consists of 500 the largest market capitalization companies in the US. This can be expanded.
- A set of documents are identified for each company. Here, I use the company's wiki page. I do this by taking the SP500 list from the previous step to get the wiki urls for each company, and then get the page id for each wiki url. This allows me to use the python wikipedia package to get the content.
- For each company, the organizations referenced within the documents (eg the wiki page) are identified using the spaCy named entity resolution (NER) package. This generates relevant and irrelevant candidates to be associated with the company.
- A probabilistic model is built to determine the association between the candidates and the company. There are many approaches, I tried the two below and ultimately went with 1 for simplicity.
- A simple model for probability is the normalized count of the organizations on the page. The drawback here is that slight variations of the company name appear infrequent, similar to completely irrelevant candidates.
- In the next level of sophistication, it is assumed that the most frequent candidate is the golden source. All candidates are compared to this with a similarity function that defines the probability of it being a relevant candidate. The drawback here is that a company with two frequent names (Alphabet and Google or Facebook and Meta) have dissimilar names.
- For each company, the list of candidates and their corresponding companies and probabilities are stored in a dictionary that is subsequently written to DynamoDb. Note that in the case a candidate appears for two different companies, the higher probability determines which company the candidate gets mapped to.
Matching Algorithm
To determine if two entities match, the illustration below demonstrates the potential cases for matching. Given the complexity, some notation is required.
- $e_i$: Entity $i$ that is input by the user for matching.
- $c_j$: Candidate $j$ are the keys of the dictionary constructed from the previous section that map to each company.
- $t_k$: The ticker or company name that is the value which candidates are mapped to.
- $P_m$ and $P_l$: The probability of an overall match and the probability of a match via look-up.
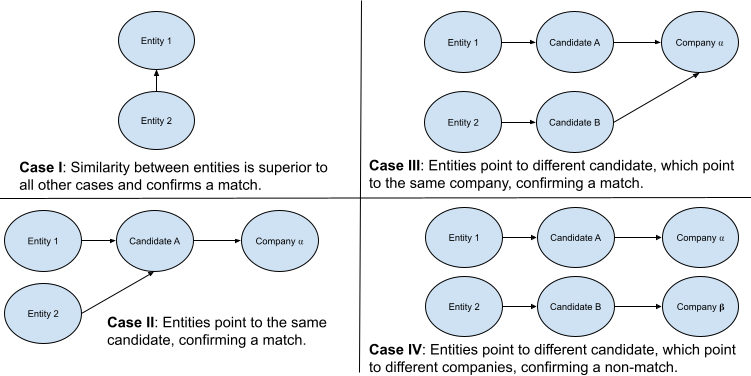
- Case I: Match. The entities themselves match with probability $P_m = P_{ee}$, which is higher than all other cases below and higher than a predefined threshold $\theta_e$.
- Case II: Match. The entities match to the same candidate, where the probability is expressed as $\min\{P_{e_1c_j}, P_{e_2c_j}\}$.
- Case III: Match. The entities match to different candidates, but the candidates map to the same company. Here, a chain rule is required. For entity $i$, the probability is $P_{e_ic_j}P_{c_jt_k}$. The minimum over each $i$ is used to represent the likelihood of the match.
- Case IV: Non-Match. The entities map to different candidates, which map to different company names. The probability is the same as case III.
- Case V (not shown): Non-Match. All other conditions will return a non-match. The fall back is Case I .
Mathematically, this is written as: $$ P_m = max\{1_{P_{ee}>\theta_e}P_{ee}, P_l\} $$ $$ P_l = \begin{cases} \min\{ P_{e_1c_j}, P_{e_2c_j} \} & Case II\\ \min\{ P_{e_1c_j}P_{c_jt_k}, P_{e_2c_j}P_{c_jt_k} \} & Case III \end{cases} $$